(come sempre, correzioni e suggerimenti sono i benvenuti)
Calcolare qual è la media di un insieme si direbbe un’operazione abbastanza tranquilla, e che non dovrebbe dare problemi di sorta: in fin dei conti, si sente parlare persino sui giornali di medie qua, medie là, e così via… Beh, è vero che non ci sono chissà quali concetti complicati dietro di essa, però è anche vero che non sempre la media per così dire naïf è la cosa che vorremmo davvero sapere; e quindi possiamo essere tranquillamente fregati da chi sa giocare con i numeri. Ecco dunque un po’ di informazioni che potranno aiutarvi a districarvi in mezzo alla media!
Innanzitutto, qual è il significato per così dire “filosofico” della media? È un valore che viene tirato fuori a partire da insieme di valori distinti. In genere questi valori sono monodimensionali: li possiamo insomma mettere in riga, come ad esempio le altezze dei ragazzi in una classe, simularli con tante barrette verticali e tirare fuori il nostro numerino. Non è detto che si possano fare proprio sempre delle barrette: se ad esempio calcoliamo la velocità media di un viaggio, abbiamo infiniti istanti di tempo su cui fare la media, e così sfruttiamo il trucco di usare spazio e tempo complessivi che sono stati percorsi invece che la velocità istantanea. Però avremmo potuto anche misurare la velocità ogni secondo e ritornare a vedere le nostre barrette. Esiste anche una media calcolata su dati multidimensionali. Un esempio non è tanto l’altezza media del territorio di una nazione (possiamo suddividerla in tanti pezzetti quadrati della stessa dimensione, e poi mettere i quadratini in fila invece che sparsi per il territorio), quanto il punto medio di una scarica di pallini contro un bersaglio.
In tutti i casi, però, capita una cosa molto importante: si perde informazione. Non c’è nulla di male, intendiamoci: la ragione principale per prendere la media è proprio il fatto che non riusciamo oppure non vogliamo gestire troppa informazione, e ci accontentiamo di una specie di Bignami. La cosa a cui dobbiamo stare attenti, però, è che non esiste il metodo giusto per prendere un unico valore, come vedremo tra poco.
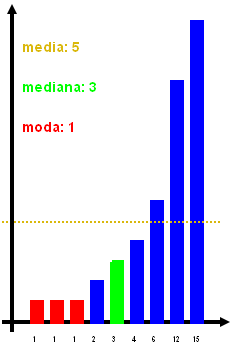
Chi fa statistica, in effetti, distingue ben tre tipi di media (in inglese, “average”); non è un loro vezzo, ma una necessità. Parleranno pertanto di media, mediana e moda: in inglese, i nomi sono rispettivamente mean, median e mode. La media è quella che tutti noi ci si aspetta, vale a dire la media aritmetica: si fa la somma dei elementi tra cui fare la media, si divide il risultato per il numero degli elementi stessi, e quello che esce fuori è la media. La mediana si calcola invece mettendo in fila tutti gli elementi, e prendendo il valore di quello di mezzo; se il numero di elementi presenti è pari, e quindi non c’è “quello di mezzo”, si prendono i due “più di mezzo” e si fa la loro media aritmetica. Resta infine la moda, detta anche norma, che è la meno intuitiva; eppure il suo significato è logico. Quando si dice che una cosa è “di moda”? Quando la usano tutti. Allo stesso modo, la moda di un gruppo di elementi è il valore che capita più spesso. Nel caso ci siano due o più valori con lo stesso numero di occorrenze, generalmente si dice che la moda non è definita; d’altra parte, se esiste, è sicuramente un valore tra quelli osservati, mentre la media non è detto lo sia e la mediana lo è sicuramente solo nel caso di un numero dispari di elementi in totale. Tanto per aggiungere un disegnino, nella figura di destra ho preso alcuni numeri (1, 1, 1, 2, 3, 4, 6, 12 e 15), li ho messi in fila belli ordinati, e ho indicato quali sono la loro media, mediana e moda.
Così a pelle ci si potrebbe chiedere che senso hanno mediana e moda, che possono essere ben lontane da quella che naturalmente associamo alla media, come possiamo ad esempio vedere nella figura qua a fianco, dove la moda è addirittura uno dei valori estremi della nostra distribuzione. Il punto è che ci sono alcuni tipi di misurazioni che conducono in maniera naturale a questi valori, solo che non ci facciamo mai caso.
Ad esempio, quando si vuole sapere se un bambino è più grande o più piccolo della media, non si guarda l’altezza media dei bambini ma si piglia la mediana, per due ottime ragioni: la prima è che i dati troppo lontani dalla norma vengono automaticamente resi irrilevanti, la seconda è che interessa appunto sapere quanti bambini sono più alti o più bassi (oppure più o meno pesanti). Addirittura il concetto di mediana si espande: perché limitarsi a dividere il nostro campione in due sole parti? Abbiamo così i
quartili (si divide il nostro gruppo in quattro parti), i decili (la divisione è in dieci parti), o i percentili (cento parti). Quindi se ti dicono che il tuo test è risultato nel novantasettesimo percentile, magari hai sbagliato metà delle domande e non puoi sapere cosa hanno fatto gli altri: però sai che solo il 3% ha fatto meglio di te, di poco o di tanto che sia.
Per la moda, pensate a quando vi dicono “il vostro biglietto è stato sorteggiato alla lotteria di Tu-campa-cavallo-al-colle. Ci sono dieci premi: uno di 10000 euro e nove di 1 euro”. Ora, è vero che la vostra vincita media è leggermente superiore ai 1000 euro; ma credo sarete d’accordo con me quando affermo che quello che potete aspettarvi è di avere vinto un euro, cioè la moda dei valori dei premi. Insomma, la moda ti serve quando non ti interessa un dato prettamente teorico come la media, ma vuoi sapere cosa ti puoi statisticamente aspettare per davvero. È roba per la gente coi piedi ben piantati in terra!
(nella prossima parte, racconterò di altri tipi di media: geometrica, armonica, mobile e pesata… Chissà se parlerò mai di cose turpi tipo varianza e skew che sono le damigelle d’onore della media!)

Ultimo aggiornamento: 2007-09-19 15:33