Sposta i cerchi

Nel diagramma qui sotto vedete sei cerchi delle stesse dimensioni, tre bianchi e tre neri. I tre cerchi bianchi sono tutti tangenti tra loro, e ciascuno dei cerchi neri è tangente a uno dei bianchi. Inoltre i cerchi neri sono inamovibili. È possibile spostare i cerchi bianchi al di fuori della zona delimitata dai cerchi neri senza sollevarli, ma facendoli solo scorrere sul piano?

   

   

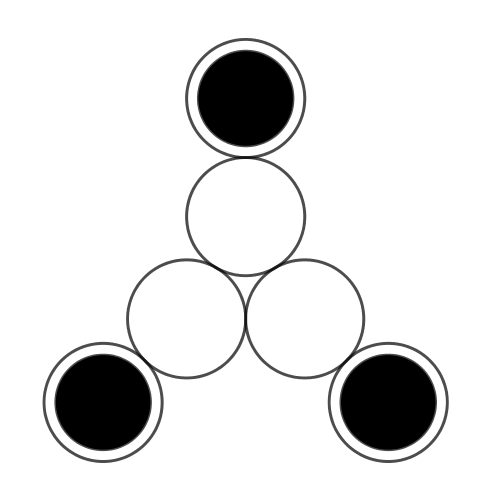
Problema tratto da Tadao Kitazawa, da Arithmetical, Geometrical and Combinatorial Puzzles from Japan.