.mau. - Matematica Light - Un teorema sudoku

Un teorema sudoku

La matematica è davvero così brutta come la dipingono? Non ne sono poi così sicuro. Mi sa tanto che quello che allontana davvero la gente dalla matematica è il fatto che non si riesce a capire perché diavolo uno dovrebbe risolvere dei problemi che tanto non gli capiteranno mai nella vita. E questo è un peccato. In fin dei conti è vero che la matematica ad alto livello è al di fuori delle possibilità di tutti noi, esattamente come la Formula 1; ma proprio come più o meno tutti noi siamo in grado di guidare un'auto, così ci sono tante dimostrazioni matematiche alla portata di tutti. L'importante è non darsi per vinti in partenza.

Per fare un esempio più vicino a quanto vediamo in giro, senza triangoli, trapezi, cerchi e quant'altro, prendiamo il sudoku. No, non spaventatevi: non vi chiedo di dimostrare quanti sono i possibili schemi - per i curiosi, sono 6.670.903.752.021.072.936.960, come specificato qua (pdf). Prendiamo semplicemente uno schema di sudoku pubblicato su un giornale, e guardiamo quanti dei numeri tra 1 e 9 sono presenti, non importa se una o più volte. Bene, il teorema che vi invito a dimostrare è il seguente: Se nello schema iniziale di un sudoku appaiono solo sette numeri diversi e il sudoku è risolvibile, allora non ha una soluzione unica (e quindi, aggiungo, non apparirà mai sui giornali, dove la soluzione è garantita essere unica).

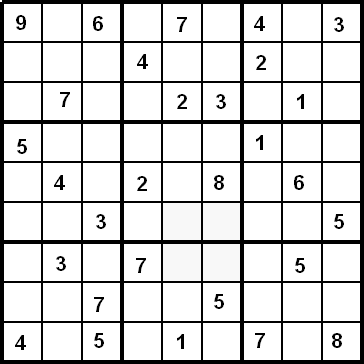
Scritto in questo modo, sembra effettivamente un risultato piuttosto complicato da dimostrare, soprattutto pensando ai seimila miliardi di miliardi di soluzioni possibili. Eppure, vi assicuro che la dimostrazione è davvero facile, se appena si è abituati a risolvere un sudoku; invito pertanto chi mi sta leggendo a pensare come potrebbe convincersi della verità del teorema. Se non siete abituati al ragionamento teorico, magari potrebbe essere utile immaginare che manchino due numeri specifici, chessò il 4 e il 9; oppure potreste cimentarvi a risolvere questo sudoku (dove tutte le cifre sono presenti, a dire il vero...) e scoprire se vi viene una qualche idea. Sotto lo schema, continuerò la trattazione e (forse) darò anche la dimostrazione del teorema.

Risolto? Siete arrivati fino in fondo? Avete capito come mai ci sono quattro caselle che non sono bianche, ma leggermente grigie? Se tutte le cose sono andate bene, e potete verificarlo ad esempio a http://sudokusolver.co.uk, tutte le caselle possono essere univocamente determinate, tranne quelle quattro. Sappiamo che ci devono essere due 4 e due 9, però possiamo scrivere 4-9 sopra e 9-4 sotto, oppure fare l'opposto, e il sudoku è comunque valido. A questo punto immagino che siate arrivati a capire cosa succede se non troviamo nessun 4 e nessun 9 in tutto lo schema iniziale: anche in questo caso, supponendo che ci sia una soluzione, ne possiamo tranquillamente scrivere un'altra scambiando di posto tutti i 4 con i 9. Visto che nello schema iniziale i due numeri non c'erano, siamo sicuri che la nuova soluzione rispetta i vincoli iniziali. Fine della dimostrazione. Sì, è proprio tutto qua: nessuno obbliga ad avere chissà quale complessità.

Vorrei però aggiungere un paio di postille. Quando ho scritto la prima versione di questo testo, mi è stato fatto notare che questa non sarebbe una "dimostrazione matematica", perché è puramente logica e il fatto che ci siano dei numeri invece che casette e fiorellini è assolutamente ininfluente. Certo che i numeri non c'entrano, ma chi è che ha detto che una dimostrazione matematica debba per forza fare dei conti? Il concetto di dimostrazione, da Euclide in poi, è puramente logico: semplicemente, è più facile applicarlo alla matematica, ma in casi come questo anche un sudoku va benissimo. La seconda cosa che vorrei fosse notata è che sono sempre stato attento a scrivere "se c'è una soluzione". La dimostrazione in effetti parte supponendo che ci sia una soluzione, e da lì mette in moto l'armamentario logico che ci porta a trovarne una seconda: ma non è affatto detto che una soluzione esista. Ad esempio, ho trovato uno schema dove solo otto caselle sono inizialmente riempite, e che non può avere nessuna soluzione (diciamo che è un esercizietto per i più vispi). Occorre insomma sempre stare attenti, quando si enuncia un teorema, a scriverlo giusto: se non avessi aggiunto la frasetta "il sudoku è risolvibile", il mio teorema sarebbe stato falso, e qualcuno mi avrebbe sicuramente sbertucciato!