La legge di Benford

distribuzione prima e ultima cifra nella popolazione dei comuni torinesi Volete fare una scommessa con i vostri amici avendo quasi la certezza di vincerla? Chiedete loro di scegliere a caso una qualunque lista di valori, purché abbastanza grande, e prendere le cifre più a sinistra. Quella più frequente sarà quasi certamente 1. Ma attenzione! Bisogna scegliere la cifra più a sinistra, non quella più a destra.
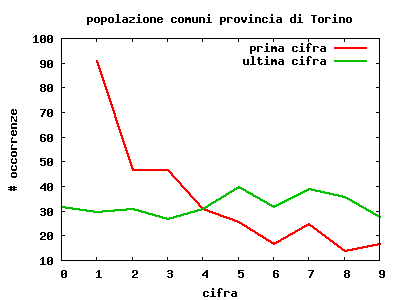
Nel disegno a fianco, ad esempio, sono mostrate la prima e l'ultima cifra della popolazione 2003 dei 315 comuni della provincia di Torino. Il grafico in verde è più o meno costante, mentre quello in rosso ha un'indubbia preferenza per la cifra 1.

Questo comportamento ha un nome ben preciso: la legge di Benford, dal nome del fisico che la presentò per primo nel 1938. Secondo tale legge, la probabilità che la prima cifra di un numero scelto "a caso" sia c è data dalla formula

B(c) = log₁₀ (c+1) - log₁₀ (c)

diagramma a torta della distribuzione della legge di Benford La dimostrazione della legge è un po' complicata, soprattutto perché bisogna definire accuratamente cosa significa "scegliere a caso": ma è abbastanza facile capire perché la cifra 1 è più frequente delle altre. Scegliamo infatti un numero a caso tra 1 ed N, per vari valori di N. Il caso peggiore è quello in cui N vale ad esempio 99; in questo caso tutte le cifre iniziali hanno la stessa probabilità. Quello migliore si ha invece quando N vale 199; in più di metà dei casi (1, da 10 a 19, da 100 a 199) il numero inizia per 1.

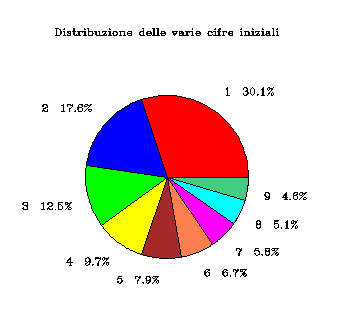
Un altro modo per intuire come la probabilità della cifra 1 sia maggiore di tutte le altre consiste nel pensare che se davvero esiste una legge, questa debba avere un'invarianza di scala; deve cioè valere se misuriamo i nostri valori in chilometri oppure in miglia. Proviamo allora a prendere una lista e raddoppiare tutti i valori: quelli che inizialmente iniziavano con una cifra tra 5 e 9 adesso inizieranno per 1. Si può quindi immaginare che la probabilità che un numero inizi per 1 sia la stessa che esso inizi per una cifra qualsiasi tra 5, 6, 7, 8 oppure 9; in effetti il diagramma a torta conferma la nostra ipotesi.

La morale di tutto questo? Non fidatevi mai di quando vi si dice che un numero è stato scelto a caso!