La legge di Benford
Sarà proprio un caso?
Facendo un giro per il sito dell'ISTAT, ho trovato una tabella con la
popolazione dei vari comuni italiani al 1. gennaio 2003. Ho preso i dati della
provincia di Torino, un po' perché è quella dove sono nato, e un po' perché è
quella che ha più comuni di tutte: ce ne sono ben 315.
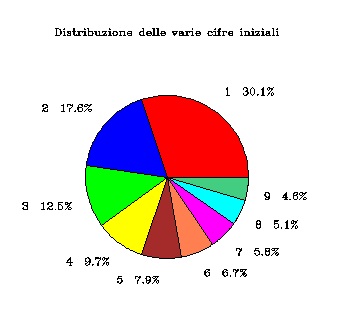
Se prendiamo la cifra più significativa, insomma quella più a sinistra, delle
315 popolazioni residenti, come sarà suddivisa? Uno può
immaginare che ci saranno più o meno lo stesso numero di occorrenze per
ciascuna delle nove cifre possibili: la media dovrebbe essere di circa 36
casi per ogni cifra.
Bene, mi sono messo a far fare i conti al mio calcolatore e il risultato
attuale lo potete vedere nella tabella 1.
Tabella 1: Frequenza della cifra più significativa della popolazione dei comuni della provincia di Torino
| cifra |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| # comuni |
91 |
47 |
47 |
31 |
26 |
17 |
25 |
14 |
17 |
|
Tabella 2: Frequenza della cifra meno significativa della popolazione dei comuni della provincia di Torino
| cifra |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| # comuni |
32 |
30 |
31 |
27 |
31 |
40 |
32 |
39 |
36 |
28 |
|
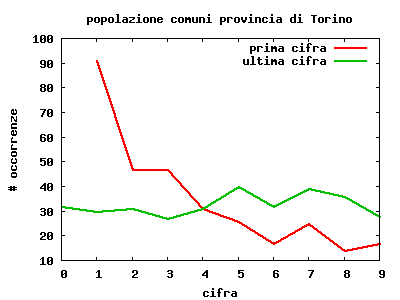 Si direbbe che c'è qualcosa che non va: la cifra 1 ha un numero di
occorrenze enorme, ben difficile da spiegarsi con una normale fluttuazione
statistica. Sembra inoltre che i valori diminuiscano man mano al crescere
della cifra iniziale, a meno di qualche caso che però potrebbe davvero
essere un errore statistico.
Si direbbe che c'è qualcosa che non va: la cifra 1 ha un numero di
occorrenze enorme, ben difficile da spiegarsi con una normale fluttuazione
statistica. Sembra inoltre che i valori diminuiscano man mano al crescere
della cifra iniziale, a meno di qualche caso che però potrebbe davvero
essere un errore statistico.
In compenso, se prendiamo l'ultima cifra delle popolazioni, cioè
quella meno significativa, otteniamo la tabella 2.
Questa volta la distribuzione sembra molto più simile a quanto uno si
aspetterebbe da una serie di numeri scelti a caso: i valori sono sparpagliati
ma non troppo. È vero che in questo caso abbiamo dieci casi e non nove, visto
che un numero può anche finire per zero, ma non credo che a nessuno venga
in mente che sia questo a fare la differenza con quello che ci è capitato
con le prime cifre. La figura a destra, che mostra entrambe le
distribuzioni, dovrebbe rendere ancora meglio l'idea.
Sarò stato così sfortunato da avere scelto un esempio fallace?
Troppe coincidenze richiedono una legge
Beh, in quel caso non sarei stato il primo a sbagliare esempio.
Verso la fine del diciannovesimo
secolo, l'astronomo Simon Newcomb fece un'osservazione casuale, di quelle che
capitano spesso quando si ha voglia di prendersi una pausa dal lavoro.
Bisogna tenere a mente che quando i computer non esistevano ancora i
"calcolatori" erano quelli che si facevano tutti i conti a mano; per
semplificare almeno un po' loro la vita venivano usati i logaritmi, che
permettono di trasformare le moltiplicazioni in addizioni, al prezzo di
consultare le "tavole dei logaritmi" che danno la conversione tra un numero
e il suo logaritmo. Newcomb, che come tutti gli astronomi aveva bisogno
di fare tanti conti, si accorse che i bordi delle prime pagine
del suo manuale erano più sporchi di quelli delle ultime pagine:
insomma, sembrava che gli capitasse più spesso
di cercare il logaritmo di un numero che iniziava con una cifra piccola.
Nel 1881 Newcomb scrisse il suo bell'articolo al riguardo ([1]), e immagino
che si sarà poi rimesso a fare l'astronomo senza più pensare alla cosa;
né ci fu nessun altro che si preoccupò della cosa, fino a che
una cinquantina d'anni più tardi il fisico Frank Benford fece la stessa
osservazione. A differenza di Newcomb, Benford
iniziò a raccogliere una grande mole di dati di tutti i tipi, magari
perché aveva ancora meno voglia di fare del lavoro serio. (A suo favore
dobbiamo aggiungere che è vero che lavorava per la General Electric, ma nei
suoi Research Laboratories, quindi poteva permettersi di fare questo
tipo di ricerche). Nel 1938 coronò la
sua fatica con un articolo ([2]) nel quale presentò i suoi dati (usando più di
20000 valori!) e formulò una legge di
distribuzione sulla prima cifra di un insieme di numeri generati casualmente
in un contesto reale. Tale legge fu poi chiamata "Legge di Benford" (non
"Legge di Newcomb": anche in matematica capita spesso che le attribuzioni
non siano sempre date al primo scopritore).
In formule, la legge afferma che la probabilità B(c) che la prima cifra
di un valore scelto a caso sia c è data da
B(c) = log10 (1 + 1/c)
Toh, di nuovo i logaritmi! Il fatto che il logaritmo sia in base 10
non è un caso: si può facilmente verificare come la legge di Benford non
valga solamente quando i numeri sono scritti in base 10, ma si può anche
usare una base di numerazione diversa: basta cambiare anche la base del
logaritmo.
Perché funziona?
 È sempre bello trovare una formuletta tanto semplice - nel senso matematico
del termine, intendo! Immagino che qualcuno sia stramazzato al suolo alla
sua vista - per descrivere un fenomeno.
Resta solo un piccolo problema: la legge è stata ricavata
in maniera empirica, e bisogna riuscire a spiegare perché mai ci debba essere
un risultato del genere.
È sempre bello trovare una formuletta tanto semplice - nel senso matematico
del termine, intendo! Immagino che qualcuno sia stramazzato al suolo alla
sua vista - per descrivere un fenomeno.
Resta solo un piccolo problema: la legge è stata ricavata
in maniera empirica, e bisogna riuscire a spiegare perché mai ci debba essere
un risultato del genere.
In fin dei conti, se fosse possibile prendere in considerazione tutti
i numeri interi, partendo da 1 e andando verso l'infinito, sembrerebbe logico
dire che tra di essi tutte le cifre iniziali appaiono con la stessa frequenza
relativa. Ma questo è puramente teorico: non
possiamo certo scegliere un numero a caso da un insieme infinito!
La considerazione qui sopra però ci dà un'idea di un possibile motivo per
cui la legge vale in pratica. I numeri che ci troviamo nella vita di
tutti i giorni hanno un limite finito, e soprattutto sono generati in ordine
crescente. La popolazione di un comune può partire da un abitante (beh, non
molto probabile, ma l'idea è quella) e crescere fino a qualche decina di
milioni. Facciamo allora un esperimento teorico: scegliamo un numero a caso
fino a un certo valore N. Se ad esempio ci capita di scegliere per N
il numero 199, più di metà delle nostre possibili scelte inizia per 1; infatti
c'è 1, i dieci numeri da 10 a 19, e i cento da 100 a 199. Certo che se
avessimo scelto N=999 il risultato sarebbe stato equo; ma sicuramente la cifra
1 non apparirà mai meno delle altre. Insomma, sembra naturale che in genere
ci siano più numeri che iniziano con una cifra piccola rispetto a una
cifra grande: quello che manca è capire perché dobbiamo avere di mezzo
proprio i logaritmi.
Il primo passo che possiamo fare per convincerci della correttezza
della legge è usare un trucco matematico standard: immaginiamo che esista
davvero una legge, e cerchiamo delle condizioni che discendono necessariamente
da essa. Beh, se la legge vale in generale per un certo insieme di valori,
deve valere anche se li raddoppiamo tutti, no? In formule, se P(x)
è la distribuzione di probabilità noi vogliamo che P(kx) = f(k)P(x).
Vi risparmio i passaggi successivi, che portano a scoprire che f(k) = 1/k
(perché l'integrale di una distribuzione di probabilità vale 1) e infine,
dopo avere differenziato l'eguaglianza, a ricavare che la soluzione dovrebbe
essere P(x) = 1/x. Peccato che questa non possa essere una vera
distribuzione di probabilità, dato che l'integrale darebbe infinito come
risultato.
A questo punto si fa uno sporco trucco e si dice "mannò, non ci
sono infinite possibilità, ma ammettiamo che il valore può arrivare solamente
fino a una certa grandezza". Per non fare preferenze, possiamo ad esempio
scegliere di andare da 1 a 999999. In questo modo riusciamo ad ottenere
un risultato finito per l'integrale: con un po' di manipolazioni algebriche
che vi risparmio riusciamo infine a tirare fuori la nostra formula.
Intendiamoci: non abbiamo dimostrato la legge, ma soltanto che se esiste
deve essere di quella forma! E in un certo senso abbiamo visto che funziona
proprio perché non possiamo scegliere a caso un numero tra gli infiniti
esistenti, ma ci dovremo sempre limitare.
Altre considerazioni
Un modo equivalente di scrivere la legge di Benford è
B(c) = log10 (c+1) - log10 (c)
Letta in questo modo, la formula ci dà un punto di vista diverso: se noi
prendessimo il logaritmo dei numeri che stiamo considerando e
guardassimo solo la parte decimale del risultato - quella che i vecchietti
come me chiamano "mantissa" - vedremmo che la prima cifra delle mantisse
è distribuita uniformemente. Ma allora ce l'abbiamo una distribuzione uniforme!
L'unico problema è che è quella dei logaritmi, e non quella dei valori
originari. Chi ha fatto un po' di statistica dovrebbe ora alzare la mano e
dire con tono saputello "distribuzione ipergeometrica!", il che significa
in pratica "le cose per cui si preferisce considerare la variazione in
percentuale, e non in differenza assoluta". Un esempio matematico? le
successive potenze di 2, oppure i numeri di Fibonacci, che infatti seguono
perfettamente la legge di Benford. (Noticina: tra i ventimila e più numeri
usati da Benford per definire la sua legge, ci sono anche queste due
successioni. Diciamo che si è aiutato un pochino per fare uscire i
risultati). Un esempio non matematico? Il valore delle azioni.
Non tutte le distribuzioni di probabilità seguono però la legge di Benford.
Se prendiamo la famosa campana di Gauss, la curva degli errori, si riesce
subito a vedere che la legge non può funzionare. Ma non tutto è perduto.
Ted Hill è infatti riuscito a dimostrare nel 1996 [4] che se si scelgono
a caso un insieme di distribuzioni di probabilità, e poi all'interno
di ciascuna di esse si sceglie a caso un numero, l'insieme di questi
valori che potremmo chiamare "casualmente casuali" obbedirà alla legge
di Benford.
Nel mio piccolo, ho provato a fare un esperimento (senza nessuna validità
scientifica, mi affretto ad aggiungere!) Ho scritto un
programmino che ha generato centomila numeri casuali tra 1 e 999999. In
effetti la prima cifra di questi numeri si distribuisce uniformemente,
come si può vedere dalla prima riga della tabella 3 qui sotto.
Il secondo passo è consistito nel
generare altri centomila numeri: questa volta essi erano compresi tra 1 e
il numero generato al passo precedente. Ho poi ripetuto la stessa operazione
altre due volte. Per fare un esempio pratico, supponiamo che il primo numero
casuale sia 724353; sceglierò il secondo tra 1 e 724353, e magari mi verrà
34121, il terzo tra 1 e 34121, e otterrò che ne so 33998, e il quarto tra 1
e 33998. I valori ottenuti sono generalmente abbastanza grandi per non
dare troppi problemi di schiacciamento dei risultati: ho scelto di partire
con un milione come primo limite proprio per questa ragione. Eppure al
quarto passo abbiamo una distribuzione di probabilità delle prime cifre che
segue quasi esattamente la legge di Benford.
Ci siamo cascati di nuovo.
Tabella 3: Risultati della simulazione di generazione numeri casuali limitati
| cifra |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| passo 1 |
11.3% | 11.1% | 11.0% | 11.2% | 11.1% | 11.0% | 11.2% | 11.1% | 11.0% |
| passo 2 |
24.2% | 18.6% | 14.3% | 11.6% | 9.6% | 7.6% | 6.1% | 4.6% | 3.4% |
| passo 3 |
30.0% | 18.9% | 13.1% | 9.8% | 7.7% | 6.4% | 5.2% | 4.6% | 4.4% |
| passo 4 |
30.9% | 17.6% | 12.4% | 9.5% | 7.7% | 6.5% | 5.6% | 5.1% | 4.7% |
Frodi fiscali
Un altro campo in cui la legge di Benford si può applicare è quello dei
bilanci aziendali. Abbiamo infatti di nuovo dei numeri più o meno casuali,
che hanno un limite superiore implicito, e che dovrebbero essere invarianti
di scala: esattamente le ipotesi che abbiamo visto più sopra.
Nei racconti sulla legge di Benford, si sente parlare spesso di Mark Nigrini,
che avrebbe smascherato dei truffatori perché i loro prelievi non seguivano
la legge. Beh, la realtà è purtroppo un po' meno romanzesca: non serviva
tutta l'analisi quando si scopre che ad esempio quasi tutti gli assegni del
presunto colpevole sono appena inferiori ai 100000 dollari, probabilmente
perché per valori superiori c'era un controllo ulteriore. Resta comunque
importante il concetto che se proprio si vuole taroccare i libri contabili,
occorre evitare di generare i numeri a caso. Il lettore che è stato
attento ha comunque intuito come si potrebbe fare a generare a caso una
serie di numeri "puliti"... e capirà perché non posso scriverlo
esplicitamente. Potrebbero incriminare anche me!
Vedi anche
Ci sono vari articoli reperibili in rete sulla legge di Benford. In italiano
si può leggere il
numero 34 di Rudi Mathematici,
l'articolo
di Ennio Peres su RES, oppure
la Wikipedia.
Chi mastica bene l'inglese (e la matematica...) ha poi le solite scelte:
Mathworld e
Mathpages.
Chi infine è più interessato a evadere le tasse farebbe meglio a leggere l'articolo di Mark
Nigrini, oppure la
pagina del sito di Nigrini.
Bibliografia
L'ho copincollata, non garantisco che gli articoli esistano veramente...
[1] Newcomb, S., "Note on the Frequency of the Use of Digits in Natural Numbers" . Amer. J. Math. 4, 39-40, 1881.
[2] Benford, F., "The Law of Anomalous Numbers". Proc. Amer. Phil. Soc. 78, 551-572, 1938.
[3] Raimi, F., "The first digit problem" . Amer. Math. Montly 83 (1976) n.7, 521-538.
[4] Hill, T. P., "A Statistical Derivation of the Significant-Digit Law" . Stat. Sci. 10, 354-363, 1996.
[5] Nigrini, M., "A Taxpayer Compliance Application of Benford's Law." , J. Amer. Tax. Assoc. 18, 72-91, 1996.
versione 1.00, 15 maggio 2009, .mau.
torna alla pagina della matematica
torna alla home page di .mau.
 Si direbbe che c'è qualcosa che non va: la cifra 1 ha un numero di
occorrenze enorme, ben difficile da spiegarsi con una normale fluttuazione
statistica. Sembra inoltre che i valori diminuiscano man mano al crescere
della cifra iniziale, a meno di qualche caso che però potrebbe davvero
essere un errore statistico.
Si direbbe che c'è qualcosa che non va: la cifra 1 ha un numero di
occorrenze enorme, ben difficile da spiegarsi con una normale fluttuazione
statistica. Sembra inoltre che i valori diminuiscano man mano al crescere
della cifra iniziale, a meno di qualche caso che però potrebbe davvero
essere un errore statistico. È sempre bello trovare una formuletta tanto semplice - nel senso matematico
del termine, intendo! Immagino che qualcuno sia stramazzato al suolo alla
sua vista - per descrivere un fenomeno.
Resta solo un piccolo problema: la legge è stata ricavata
in maniera empirica, e bisogna riuscire a spiegare perché mai ci debba essere
un risultato del genere.
È sempre bello trovare una formuletta tanto semplice - nel senso matematico
del termine, intendo! Immagino che qualcuno sia stramazzato al suolo alla
sua vista - per descrivere un fenomeno.
Resta solo un piccolo problema: la legge è stata ricavata
in maniera empirica, e bisogna riuscire a spiegare perché mai ci debba essere
un risultato del genere.