0,999999... = 1

Tra le domande che mi vengono fatte "visto che tu sei matematico", ce n'è una che mi arriva abbastanza spesso; confesso però che non sono mai riuscito a capire perché mai la gente la trovi così interessante. La domanda, come avrete intuito dal titolo, è "Ma è proprio vero che 0,999999... con tutti 9 fino all'infinito è uguale a 1"? Non so in effetti quale sia la molla che scatta a chi me lo chiede: forse c'è il concetto dell'infinito potenziale che non si può mai raggiungere, forse echi nascosti del paradosso di Achille e della Tartaruga, forse i giochettini con la calcolatrice "scrivi 1/3*3 e vedi che cosa succede...", o chissà cos'altro. Poi intendiamoci: la domanda è perfettamente lecita, visto che la risposta (sì, per quelli che non hanno voglia di leggere fino in fondo) è stata formalizzata in maniera completa solo da 150 anni; addirittura, se si vuole essere alternativi a tutti i costi, si potrebbe anche dire che la risposta è "no": ma quello sarà l'argomento di un altro mio articolo.

Se ci si fida delle formulette pratiche, basta usare quella che si studiava alle medie ai miei tempi, e che vi presento qua nella sua versione più semplice, quella per convertire in frazione un numero della forma 0,abc...lmabc...lm..., cioè compreso tra 0 e 1, e con il periodo formato dalle cifre abc...lm. Se la lunghezza di questo periodo è di k cifre, basta avere una frazione che a numeratore abbia il periodo e a denominatore un numero formato ripetendo k volte la cifra 9. Come esempio pratico, 0,142857142857142... è uguale a 142857/999999, cioè a 1/7. E 0,999999...? Il periodo è di una sola cifra, la regoletta mi dice di fare 9/9, cioè 1. Ma magari uno della formuletta non si fida, e vuole andare più a fondo nella questione.

Un po' di storia

Comincio allora con una provocazione. Innanzitutto, ha senso parlare di 0,999999...? Qualcuno è capace a misurare 0,999999... metri, o sintonizzare una radio a 0,999999... megahertz? Ovviamente no. (Tranne Chuck Norris, mi hanno fatto notare!) Ogni misurazione ha in effetti una sua precisione specifica e un margine di errore; quindi la domanda iniziale, in un certo senso, è assolutamente inutile all'atto pratico. Addirittura i fisici ci dicono da quasi un secolo che non è possibile avere una precisione infinita, per il principio di indeterminazione di Heisenberg: insomma, la domanda è del tutto teorica. Ma questo non sarebbe un grave problema, visto che in fin dei conti qui stiamo parlando di matematica e non del mondo reale. Più interessante è un'altra obiezione, quella che fa notare che scrivere un numero con la virgola è un concetto piuttosto moderno.
[alcuni
valori sulla retta dei numeri] Gli arabi introdussero la notazione dei numeri con la virgola nel XV secolo; la notazione apparve in Europa (probabilmente in maniera indipendente) per opera di Simon Stevin nel 1585, ma non si diffuse realmente fino a dopo la rivoluzione francese, quando il sistema metrico decimale le diede la spinta finale. Pensateci su: se io dico 0,1 kilometri si capisce subito di che distanza sto parlando (sono cento metri), ma dire 0,1 miglia (176 iarde, o 528 piedi) significa ben poco, per chi i conti li fa in piedi e iarde! Non è un caso che la formuletta mostrata sopra converta un numero periodico in una frazione; per le attività pratiche, le frazioni sono molto più semplici da visualizzare, e non è un caso che ore e minuti siano divise in sessanta parti e i giorni in 24 ore. Il fatto che un terzo di ora siano 0,3333333.... ore non dà fastidio a nessuno, visto che tutti pensano immediatamente a venti minuti e di puntini all'infinito non ce ne sono per nulla. L'ultima cosa su cui sono più o meno d'accordo tutti è che i numeri si possono mettere belli ordinati su una retta, che viene appunto chiamata retta dei numeri. Se pensiamo a un metro di quelli da muratore o da sarto, oppure a un termometro analogico così che ci siano anche i numeri negativi, l'idea è chiarissima; magari facciamo un po' fatica a collocare esattamente pi greco, ma la cosa non ci turba più di tanto perché immaginiamo che sia un poco a destra del 3, e se prendiamo una lente d'ingrandimento lo possiamo collocare in maniera ancora più precisa.

Diamoci un taglio!

Adesso sappiamo che i numeri con la virgola hanno sì e no duecento anni di uso pratico. Ma i numeri con infinite cifre dopo la virgola sono ancora più giovani, in effetti, e sono un prodotto di un complicato sforzo per capire cosa sono esattamente i numeri reali; numeri che venivano allegramente usati da secoli in analisi matematica senza che nessuno fosse poi realmente sicuro di cosa stava facendo. Questa sezione è un po' più complicata: potete tranquillamente saltarla e passare alla successiva, se vi sentite troppo male.

Dopo tutti quei secoli di tentativi, alla fine fu Richard Dedekind a tirare fuori una soluzione accettata da praticamente tutti i matematici, che permette di definire un numero reale per mezzo dei numeri razionali; per la precisione, da due insiemi di razionali. Il modo che si usa di solito per spiegare come si fanno queste successioni è il definire la radice quadrata di due. Si prendono tutti i numeri razionali positivi e li si mettono in due insiemi: quelli il cui quadrato è maggiore o uguale a due, e quelli il cui quadrato è minore di due. Sì, lo so che non c'è un numero razionale il cui quadrato sia due, ma questo non è un problema, come vedremo.

Chiamiamo i due insiemi T+ e T-, e aggiungiamo tutti i razionali negativi e lo zero in T-. A questo punto abbiamo due insiemi - due semirette, se preferiamo guardare la retta dei numeri - tali che:

ogni numero razionale appartiene ad esattamente uno dei due insiemi
tutti i numeri dell'insieme T- sono minori di ciascun numero dell'insieme T+

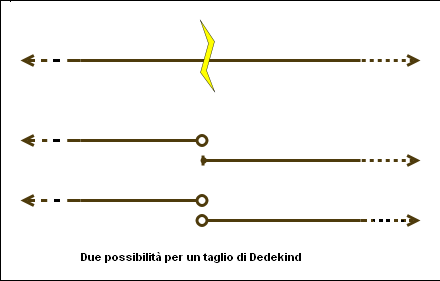Una suddivisione dei numeri razionali che rispecchi queste due caratteristiche si chiama taglio di Dedekind; la ragione del nome è chiara, se si pensa alla retta dei numeri e a un coltello molto affilato che la tagli in due parti. Il genio di Dedekind sta nell'avere affermato che i due insiemi sono un numero; se preferite essere un po' più formali bisognerebbe dire che "rappresentano" un numero, ma un vero matematico non si preoccupa di tali distinguo formali. Un matematico si preoccupa solo che le definizioni siano corrette e coerenti: che cioè esistano delle operazioni "somma" e "prodotto" tali che "sommare" e "moltiplicare" due suddivisioni diano una suddivisione che corrisponda alla somma e al prodotto dei due numeri corrispondenti; e che se due numeri sono uguali anche i due insiemi corrispondenti lo siano. Vi risparmio tutta la parte tecnica di verifica di queste cose; l'unica cosa che è davvero interessante è che a volte capita che l'insieme dei numeri più piccoli abbia un massimo, a volte capita che l'insieme dei numeri più grandi abbia un minimo, e altre volte nessuno dei due insiemi ha un limite, come nel caso di T+ e T- che abbiamo visto sopra.

Non può capitare il caso che entrambi gli insiemi abbiano rispettivamente un massimo e un minimo. Infatti questi due valori devono essere distinti, altrimenti il numero apparterrebbe a entrambi gli insiemi; ma a questo punto possiamo prendere la media tra i due valori, che sarà un numero che non può appartenere a nessuno degli insiemi, e ciò non è possibile.

Finalmente ci siamo. I numeri razionali sono tutti e soli quelli per cui nella rappresentazione con i due insiemi uno di essi ha un limite; e quel limite è il nostro buon vecchio numero razionale. Tutto quello che rimane d'altro sono i numeri irrazionali; sappiamo dai tempi di Pitagora che ci sono, e siamo finalmente riusciti a disegnarli sulla retta dei numeri. D'accordo, sto barando un po' perché dovrei anche dimostrare che in questo modo abbiamo finito tutti i numeri che possiamo trovare sulla nostra retta; posso garantirvi però che il modello di Dedekind ci assicura anche quello, sfruttando il principio di Archimede.

No, il principio non è quello dell'"eureka" mentre faceva il bagno, ma una proprietà che dice che dati due numeri positivi a e b, è sempre possibile trovare un multiplo di a che sia maggiore di b. Prendiamo ora i due insiemi U-, definito come "tutti i numeri minori di 1" e U+, "tutti i numeri maggiori a 1". Nell'insieme U- troviamo 0,9, 0,99, 0,999, .... e anche il nostro 0,999999... deve stare lì, visto che sicuramente non può essere maggiore di 1. U+ e U- non formano un taglio di Dedekind, perché lasciano fuori 1, ma da qualunque parte noi lo mettiamo otteniamo il nostro bel taglio, che per quanto detto sopra equivale al numero 1. Insomma, ce l'abbiamo fatta! (almeno fino al mio prossimo articolo)

Ricapitolando

Perché insomma possiamo dire che 0,999999...=1? Beh, abbiamo sfruttato fondamentalmente due cose. Il principio di Archimede, che possiamo anche esprimere dicendo "se prendiamo abbastanza granelli di sabbia possiamo fare un mucchio grande a piacere", e che ci dice che se due numeri sono diversi, la loro differenza può essere ingrandita fino a superare una quantità a piacere; e il "modello standard" della retta dei numeri, che unito al taglio di Dedekind ci dice che se siamo sicuri di non aver lasciato nulla da parte siamo per forza arrivati allo stesso numero. Aggiungo, per chi si fosse perso per strada, che di per sé il fatto che esistano dei numeri irrazionali non c'entra nulla con la dimostrazione, anche se ce lo siamo trovati come bonus mentre facevamo i tagli di Dedekind: una conferma insomma della formuletta all'inizio che ci diceva che 0,999999... era in realtà una frazione. Per il momento è tutto, ma aspettatevi qualcosa di completamente diverso!