Si fa presto a dire media
Calcolare qual è la media di un insieme si direbbe un'operazione
abbastanza tranquilla, e che non dovrebbe dare problemi di sorta: in fin
dei conti, si sente parlare persino sui giornali di medie qua, medie là,
e così via... Beh, è vero che non ci sono chissà quali concetti complicati
dietro di essa, però è anche vero che non sempre la media per così dire
naïf è la cosa che vorremmo davvero sapere; e quindi possiamo essere
tranquillamente fregati da chi sa giocare con i numeri. Ecco dunque
un po' di informazioni che potranno aiutarvi a districarvi in mezzo
alla media!
La media è un sistema per ridurre i dati
Innanzitutto, qual è il significato per così dire "filosofico"
della media? È un valore che viene tirato fuori a partire da insieme di
valori distinti. In genere questi valori sono monodimensionali:
li possiamo insomma mettere in riga, come ad esempio le altezze dei
ragazzi in una classe, simularli con tante barrette verticali e tirare
fuori il nostro numerino. Non è detto che si possano fare proprio
sempre delle barrette: se ad esempio calcoliamo la velocità media di
un viaggio, abbiamo infiniti istanti di tempo su cui fare la media, e
così sfruttiamo il trucco di usare spazio e tempo complessivi che sono
stati percorsi invece che la velocità istantanea. Però avremmo potuto
anche misurare la velocità ogni secondo e ritornare a vedere le nostre
barrette. Esiste anche una media calcolata su dati multidimensionali. Un
esempio non è tanto l'altezza media del territorio di una nazione
(possiamo suddividerla in tanti pezzetti quadrati della stessa dimensione,
e poi mettere i quadratini in fila invece che sparsi per il territorio),
quanto il punto medio di una scarica di pallini contro un bersaglio.
In tutti i casi, però, capita una cosa molto importante: si
perde informazione. Non c'è nulla di male, intendiamoci: la ragione
principale per prendere la media è proprio il fatto che non riusciamo
oppure non vogliamo gestire troppa informazione, e ci accontentiamo
di una specie di Bignami. La cosa a cui dobbiamo stare attenti, però,
è che non esiste il metodo giusto per prendere un unico valore,
come vedremo tra poco.
Media, mediana, moda
 Chi fa statistica, in effetti, distingue ben tre tipi di media (in
inglese, "average"); non è un loro vezzo, ma una necessità. Parleranno
pertanto di media, mediana e moda: in inglese, i
nomi sono rispettivamente mean, median e mode. La
media è quella che tutti noi ci si aspetta, vale a dire la media
aritmetica: si fa la somma dei elementi tra cui fare la media, si
divide il risultato per il numero degli elementi stessi, e quello che
esce fuori è la media. La mediana si calcola invece mettendo in
fila tutti gli elementi, e prendendo il valore di quello di mezzo; se il
numero di elementi presenti è pari, e quindi non c'è "quello di mezzo",
si prendono i due "più di mezzo" e si fa la loro media aritmetica. Resta
infine la moda, detta anche norma, che è la meno intuitiva;
eppure il suo significato è logico. Quando si dice che una cosa è "di
moda"? Quando la usano tutti. Allo stesso modo, la moda di un gruppo
di elementi è il valore che capita più spesso. Nel caso ci siano due
o più valori con lo stesso numero di occorrenze, generalmente si dice
che la moda non è definita; d'altra parte, se esiste, è sicuramente
un valore tra quelli osservati, mentre la media non è detto lo sia e la
mediana lo è sicuramente solo nel caso di un numero dispari di elementi in
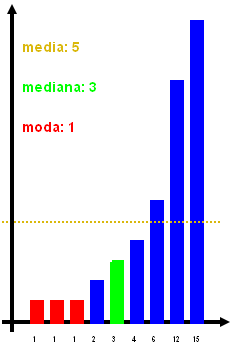
totale. Tanto per aggiungere un disegnino, nella figura di destra ho preso
alcuni numeri (1, 1, 1, 2, 3, 4, 6, 12 e 15), li ho messi in fila belli
ordinati, e ho indicato quali sono la loro media, mediana e moda.
Chi fa statistica, in effetti, distingue ben tre tipi di media (in
inglese, "average"); non è un loro vezzo, ma una necessità. Parleranno
pertanto di media, mediana e moda: in inglese, i
nomi sono rispettivamente mean, median e mode. La
media è quella che tutti noi ci si aspetta, vale a dire la media
aritmetica: si fa la somma dei elementi tra cui fare la media, si
divide il risultato per il numero degli elementi stessi, e quello che
esce fuori è la media. La mediana si calcola invece mettendo in
fila tutti gli elementi, e prendendo il valore di quello di mezzo; se il
numero di elementi presenti è pari, e quindi non c'è "quello di mezzo",
si prendono i due "più di mezzo" e si fa la loro media aritmetica. Resta
infine la moda, detta anche norma, che è la meno intuitiva;
eppure il suo significato è logico. Quando si dice che una cosa è "di
moda"? Quando la usano tutti. Allo stesso modo, la moda di un gruppo
di elementi è il valore che capita più spesso. Nel caso ci siano due
o più valori con lo stesso numero di occorrenze, generalmente si dice
che la moda non è definita; d'altra parte, se esiste, è sicuramente
un valore tra quelli osservati, mentre la media non è detto lo sia e la
mediana lo è sicuramente solo nel caso di un numero dispari di elementi in
totale. Tanto per aggiungere un disegnino, nella figura di destra ho preso
alcuni numeri (1, 1, 1, 2, 3, 4, 6, 12 e 15), li ho messi in fila belli
ordinati, e ho indicato quali sono la loro media, mediana e moda.
Così a pelle ci si potrebbe chiedere che senso hanno mediana e moda, che possono
essere ben lontane da quella che naturalmente associamo alla media, come
possiamo ad esempio vedere nella figura qua a fianco, dove la moda è addirittura
uno dei valori estremi della nostra distribuzione. Il punto è che ci sono alcuni
tipi di misurazioni che conducono in maniera naturale a questi valori, solo che
non ci facciamo mai caso. Ad esempio, quando si vuole sapere se un bambino è più
grande o più piccolo della media, non si guarda l'altezza media dei bambini ma
si piglia la mediana, per due ottime ragioni: la prima è che i dati troppo
lontani dalla norma vengono automaticamente resi irrilevanti, la seconda è che
interessa appunto sapere quanti bambini sono più alti o più bassi (oppure
più o meno pesanti). Addirittura il concetto di mediana si espande: perché
limitarsi a dividere il nostro campione in due sole parti? Abbiamo così i
quartili (si divide il nostro gruppo in quattro parti), i decili
(la divisione è in dieci parti), o i percentili (cento parti). Quindi se
ti dicono che il tuo test è risultato nel novantasettesimo percentile, magari
hai sbagliato metà delle domande e non puoi sapere cosa hanno fatto gli altri:
però sai che solo il 3% ha fatto meglio di te, di poco o di tanto che sia.
Per la moda, pensate a quando vi dicono "il vostro biglietto è stato sorteggiato
alla lotteria di Tu-campa-cavallo-al-colle. Ci sono dieci premi: uno di 10000
euro e nove di 1 euro". Ora, è vero che la vostra vincita media è
leggermente superiore ai 1000 euro; ma credo sarete d'accordo con me quando
affermo che quello che potete aspettarvi è di avere vinto un euro, cioè la moda
dei valori dei premi. Insomma, la moda ti serve quando non ti interessa un dato
prettamente teorico come la media, ma vuoi sapere cosa ti puoi statisticamente
aspettare per davvero. È roba per la gente coi piedi ben piantati in terra!
Qualche altra media
Non penserete mica di esservela cavata, con le medie? Ne sono state definite di
tutti i tipi, sempre per la solita ragione che in alcuni casi conviene usare una
definizione diversa da quella abituale. Eccovi allora qualche altro tipo di
media più esoterica: non garantisco che vi serviranno nella vita di tutti i
giorni, ma magari vi permetterà di fare bella figura in società!
La media geometrica è l'evoluzione della media aritmetica, nel senso che
invece che avere somma e divisione si usano il prodotto e l'estrazione di
radice. Limitandoci a due termini a e b, la loro media geometrica
è data da √(ab); inutile dire che se i termini fossero stati N, avremmo
usato la radice N-sima. Il nome di questa media credo derivi dal fatto che se
abbiamo un rettangolo di lati a e b, il quadrato della stessa area
ha appunto come lato √(ab); quindi ti permette di dire qual è il
"segmento medio" quando pensiamo all'area di una figura. Se vogliamo vedere la
cosa in un altro modo e nascondere le radici quadrate, possiamo dirla così: se
a è la media aritmetica tra m e n, allora n-a =
a-m. Se g è la media geometrica tra m e n, allora
n/g = g/m.
La media armonica è più complicata da spiegare, visto che è "l'inverso
della media aritmetica degli inversi". Nel caso di due elementi, la formula si
semplifica un po', visto che da 1/((1/2)((1/a)+(1/b))) si può
arrivare a scrivere 2ab/(a+b); la fregatura è che nessuno
si ricorda mai la formula "semplice", e quindi si deve tutte le volte manipolare
quella "complicata", ma sicuramente più logica. Mi sarebbe piaciuto poter dire
che la media armonica serve per trovare la "nota di mezzo" tra due, ma un po' di
conti fanno subito vedere che non è sempre vero. La media armonica tra un do e
quello successivo sulla scala, ad esempio, è un fa e non un fa diesis; la media
armonica tra un do e il sol superiore è però effettivamente un mi bemolle, il
che ci rende un po' più felici. Ma niente paura: esiste davvero un tipo di
misura per cui la media armonica è quella naturale. Supponiamo che abbia guidato
per 10 chilometri alla velocità media di 30 Km/h e per altri 10 chilometri alla
velocità media di 60 Km/h: quale sarà la velocità media complessiva? 45 all'ora?
No. La media aritmetica sarebbe stata la risposta giusta se avessi guidato per
dieci minuti alle due velocità: allora avrei percorso complessivamente 15
chilometri in venti minuti, e i conti sarebbero tornati. Invece ho impiegato
venti minuti per fare il primo tratto e dieci per fare il secondo tratto; in
tutto sono stato in auto per mezz'ora e ho percorso 20 km, con una media
complessiva di 40 Km/h, che guarda caso è la media armonica di 30 e 60. Questa
differenza è tra l'altro alla base di un problemino matematico semplice ma
fuorviante. Supponiamo che io voglia percorrere i 200 Km tra Milano e Bologna
alla velocità media di 80 Km/h, ma visto il traffico sull'Autosole sia costretto
a fare i primi 100 chilometri ai quaranta all'ora. Se d'improvviso dopo Parma
sono spariti tutti, a che velocità devo andare per il resto del percorso per
raggiungere la media che volevo fare all'inizio?
 Anche gli ingegneri, poi, non volevano essere da meno e si
sono inventati ancora un altro tipo di media, che chiamano media
quadratica oppure valore efficace. Questo tipo di media è
utile ad esempio nel caso si voglia calcolare la media di tensione della
corrente alternata. La fregatura della corrente alternata è che a volte
la tensione è positiva e a volte negativa: se si fa la media aritmetica
viene fuori zero, e chiunque si sia preso una scossa capisce che c'è
qualcosa che non va. Un approccio naïf potrebbe essere quello di prendere
il valore assoluto di tensione e fare la media di quello; ma gli ingegneri
- nonostante affermino il contrario - non amano le semplificazioni e
hanno così pensato a un approccio più complicato. Per calcolare la media
quadratica si prendono i vari valori, li si eleva al quadrato
(capito il motivo del nome?), si fa la media dei nuovi valori ottenuti
e si estrae la radice quadrata del tutto. In effetti, a dirla così, la
cosa sembra davvero un'inutile complicazione: ma gli ingegneri hanno un
asso nella manica e dicono che questo tipo di media tiene anche in conto
quanto i dati sono dispersi... ma di questo ne parlerò un'altra volta,
anche perché dire il vero non è che la cosa mi convinca troppo.
Anche gli ingegneri, poi, non volevano essere da meno e si
sono inventati ancora un altro tipo di media, che chiamano media
quadratica oppure valore efficace. Questo tipo di media è
utile ad esempio nel caso si voglia calcolare la media di tensione della
corrente alternata. La fregatura della corrente alternata è che a volte
la tensione è positiva e a volte negativa: se si fa la media aritmetica
viene fuori zero, e chiunque si sia preso una scossa capisce che c'è
qualcosa che non va. Un approccio naïf potrebbe essere quello di prendere
il valore assoluto di tensione e fare la media di quello; ma gli ingegneri
- nonostante affermino il contrario - non amano le semplificazioni e
hanno così pensato a un approccio più complicato. Per calcolare la media
quadratica si prendono i vari valori, li si eleva al quadrato
(capito il motivo del nome?), si fa la media dei nuovi valori ottenuti
e si estrae la radice quadrata del tutto. In effetti, a dirla così, la
cosa sembra davvero un'inutile complicazione: ma gli ingegneri hanno un
asso nella manica e dicono che questo tipo di media tiene anche in conto
quanto i dati sono dispersi... ma di questo ne parlerò un'altra volta,
anche perché dire il vero non è che la cosa mi convinca troppo.
Quello che invece è interessante notare è che non solo se si
prendono due numeri positivi tutte queste medie sono diverse tra loro
- a meno che i due numeri siano uguali tra loro, ma allora a che ti
serve farne la media? - ma sono sempre in un ben preciso ordine di
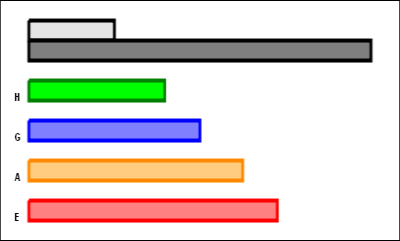
grandezza relativa. Nella figura a fianco, potete vedere cosa succede:
dati due numeri (quelli in grigio in alto: rispettivamente 6 e 24)
la media minore è quella armonica H, che nel nostro caso vale
9.6; segue la media geometrica G, che vale 12; poi c'è quella
aritmetica A, che è 15; infine si ha la media quadratica E, che
vale .306 e cioè quasi 17.5. Anche se in questo esempio le varie medie
sembrano essere tutte ugualmente distanziate tra di loro, questo è un
caso; quello che come dicevo non è casuale è l'ordine relativo tra le
medie, che è sempre lo stesso. Addirittura per quanto riguarda la media
aritmetica e geometrica, che sono le due più usate, la cosa assume il
nome pomposo di disuguaglianza aritmetico-geometrica.
Medie giornalistiche
Ci sono ancora due tipi di media che si possono trovare leggendo i giornali;
anch'esse hanno in fin dei conti diritto di esistenza, e quindi mi pare giusto
parlarne un po'. La media pesata si usa... quando si vogliono confrontare
mele con pere. No, non è così, ma l'idea è abbastanza simile. Supponiamo di
volere calcolare il reddito medio degli italiani, partendo dal reddito medio
degli abitanti delle varie regioni. La prima idea potrebbe essere quella di fare
la media dei vari redditi. Però la Provincia Autonoma di Bolzano, con meno di
mezzo milione di abitanti, ha un reddito quasi triplo della Sicilia, che di
abitanti ne ha dieci volte tanto; fare una semplice media funziona peggio
dell'esempio di Trilussa del mezzo pollo. Se non ci credete, provate a pensare a
due gruppi, uno con dieci persone che non hanno un euro e uno con una singola
persona che possiede ben dieci euro; la media non è certo di cinque euro a
testa!
 Il trucco per ottenere un dato sensato è moltiplicare
il reddito medio delle singole regioni per il numero di abitanti
della regione stessa, fare la media (aritmetica) dei risultati, e
dividere il totale per il numero complessivo degli abitanti
italiani. Abbiamo pertanto dato un "peso" ai singoli valori, peso
calcolato sul numero di abitanti. Scritto così sembra chissà che cosa,
ma concettualmente non è che sia poi così complicato: se il reddito
medio degli altoatesini è di 40000 euro, e il numero di cittadini è
mezzo milione, questo significa che è come se ciascuno di loro avesse
quel reddito. Facendo quindi la moltiplicazione otteniamo il reddito
totale della Provincia Autonoma, che si può sommare a quello delle
altre regioni perché "sono tutte mele" (non c'è la parola "media"). Ma
visto che la media dobbiamo alla fine farla, ecco che dopo occorre fare
una divisione. Detto in un altro modo, la media pesata è una banale media,
dove non si prende un singolo rappresentante per ogni elemento del nostro
insieme, ma li si prende tutti, ovviamente dando loro lo stesso valore
perché è l'unico che conosciamo. Il bello della media è che è vero che la
distribuzione dei redditi tra le singole persone è molto disuguale, ma per
fare i conti possiamo fare finta che siano tutti uguali: basta ricordarsi
di prenderli però tutti, e non limitarsi a un solo rappresentante.
Il trucco per ottenere un dato sensato è moltiplicare
il reddito medio delle singole regioni per il numero di abitanti
della regione stessa, fare la media (aritmetica) dei risultati, e
dividere il totale per il numero complessivo degli abitanti
italiani. Abbiamo pertanto dato un "peso" ai singoli valori, peso
calcolato sul numero di abitanti. Scritto così sembra chissà che cosa,
ma concettualmente non è che sia poi così complicato: se il reddito
medio degli altoatesini è di 40000 euro, e il numero di cittadini è
mezzo milione, questo significa che è come se ciascuno di loro avesse
quel reddito. Facendo quindi la moltiplicazione otteniamo il reddito
totale della Provincia Autonoma, che si può sommare a quello delle
altre regioni perché "sono tutte mele" (non c'è la parola "media"). Ma
visto che la media dobbiamo alla fine farla, ecco che dopo occorre fare
una divisione. Detto in un altro modo, la media pesata è una banale media,
dove non si prende un singolo rappresentante per ogni elemento del nostro
insieme, ma li si prende tutti, ovviamente dando loro lo stesso valore
perché è l'unico che conosciamo. Il bello della media è che è vero che la
distribuzione dei redditi tra le singole persone è molto disuguale, ma per
fare i conti possiamo fare finta che siano tutti uguali: basta ricordarsi
di prenderli però tutti, e non limitarsi a un solo rappresentante.
 La media mobile si può trovare spesso nelle pagine di
economia. Prendiamo il valore di un'azione quotata in borsa. Soprattutto
se l'azione non è una delle più trattate, da un giorno all'altro ci
sono spesso delle variazioni consistenti, che però alla lunga più o
meno si annullano. Oppure consideriamo il numero di copie vendute da un
giornale - o il numero di lettori del mio blog. Un quotidiano sportivo
vende molte più copie il lunedì, mentre per un quotidiano economico il
lunedì è una giornata morta; i miei pochi lettori durante il weekend
hanno generalmente qualcosa di meglio da fare che vedere se ho scritto
qualcosa... o più probabilmente durante la settimana sono così scazzati
che pur di fare qualcosa si mettono a leggermi. In ogni caso, il valore di
un singolo giorno ha un'importanza relativa, se voglio sapere la tendenza
sul lungo periodo. Bene, il sistema più semplice per ridurre l'influsso
di valori spuri è quello di calcolare la media su un numero prefissato
di valori: sette giorni nel caso del giornale, magari un intero mese per
il titolo azionario. Nel primo caso, la variabilità delle quotazioni
è semplicemente nascosta dal grande numero di dati usati; nel secondo
caso il ragionamento logico che si fa ha una sua correttezza formale,
perché confronti dati coerenti, anche se si spostano (ecco il perché la
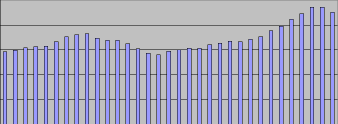
media si chiama "mobile"!) nel tempo. Le due tabelle disegnate qui sopra
mostrano il numero di accessi al mio blog nelle ultime sei settimane;
converrete che è molto più semplice vedere qual è la tendenza guardando
la media mobile settimanale a sinistra, piuttosto che con il grafico
giornaliero a destra. Abbiamo ancora una volta di fronte a noi il
potere della media: eliminare dettagli inutili per la nostra analisi,
e permetterci di concentrarci su quello che ci interessa realmente.
La media mobile si può trovare spesso nelle pagine di
economia. Prendiamo il valore di un'azione quotata in borsa. Soprattutto
se l'azione non è una delle più trattate, da un giorno all'altro ci
sono spesso delle variazioni consistenti, che però alla lunga più o
meno si annullano. Oppure consideriamo il numero di copie vendute da un
giornale - o il numero di lettori del mio blog. Un quotidiano sportivo
vende molte più copie il lunedì, mentre per un quotidiano economico il
lunedì è una giornata morta; i miei pochi lettori durante il weekend
hanno generalmente qualcosa di meglio da fare che vedere se ho scritto
qualcosa... o più probabilmente durante la settimana sono così scazzati
che pur di fare qualcosa si mettono a leggermi. In ogni caso, il valore di
un singolo giorno ha un'importanza relativa, se voglio sapere la tendenza
sul lungo periodo. Bene, il sistema più semplice per ridurre l'influsso
di valori spuri è quello di calcolare la media su un numero prefissato
di valori: sette giorni nel caso del giornale, magari un intero mese per
il titolo azionario. Nel primo caso, la variabilità delle quotazioni
è semplicemente nascosta dal grande numero di dati usati; nel secondo
caso il ragionamento logico che si fa ha una sua correttezza formale,
perché confronti dati coerenti, anche se si spostano (ecco il perché la
media si chiama "mobile"!) nel tempo. Le due tabelle disegnate qui sopra
mostrano il numero di accessi al mio blog nelle ultime sei settimane;
converrete che è molto più semplice vedere qual è la tendenza guardando
la media mobile settimanale a sinistra, piuttosto che con il grafico
giornaliero a destra. Abbiamo ancora una volta di fronte a noi il
potere della media: eliminare dettagli inutili per la nostra analisi,
e permetterci di concentrarci su quello che ci interessa realmente.
Per calcolare la media mobile su una finestra di N valori, occorre
salvarsi tutti gli ultimi N+1 valori. Il procedimento banale consiste
nel sommare gli N numeri e poi dividere per N, ma nel caso N sia grande
il calcolo potrebbe dimostrarsi tedioso. Un sistema molto più semplice
è prendere il valore della media attuale, e sommargli un N-simo della
differenza tra il valore attuale e quello a distanza N. Chi ha voglia
di fare i conti può vedere come il conto equivale a buttare via il
valore più vecchio e mettere al suo posto quello appena trovato, che
poi è l'operazione che si vede capitare se ritagliamo una finestrella
da un pezzo di carta, la posizioniamo sul foglio con i nostri dati e la
spostiamo di una posizione a destra. Come sempre, nulla di complicato,
almeno fino a che non te lo nascondono dietro una serie di paroloni!
©
Maurizio Codogno, 27 novembre 2007
torna a .mau. —
matematica. —
light
 Chi fa statistica, in effetti, distingue ben tre tipi di media (in
inglese, "average"); non è un loro vezzo, ma una necessità. Parleranno
pertanto di media, mediana e moda: in inglese, i
nomi sono rispettivamente mean, median e mode. La
media è quella che tutti noi ci si aspetta, vale a dire la media
aritmetica: si fa la somma dei elementi tra cui fare la media, si
divide il risultato per il numero degli elementi stessi, e quello che
esce fuori è la media. La mediana si calcola invece mettendo in
fila tutti gli elementi, e prendendo il valore di quello di mezzo; se il
numero di elementi presenti è pari, e quindi non c'è "quello di mezzo",
si prendono i due "più di mezzo" e si fa la loro media aritmetica. Resta
infine la moda, detta anche norma, che è la meno intuitiva;
eppure il suo significato è logico. Quando si dice che una cosa è "di
moda"? Quando la usano tutti. Allo stesso modo, la moda di un gruppo
di elementi è il valore che capita più spesso. Nel caso ci siano due
o più valori con lo stesso numero di occorrenze, generalmente si dice
che la moda non è definita; d'altra parte, se esiste, è sicuramente
un valore tra quelli osservati, mentre la media non è detto lo sia e la
mediana lo è sicuramente solo nel caso di un numero dispari di elementi in
totale. Tanto per aggiungere un disegnino, nella figura di destra ho preso
alcuni numeri (1, 1, 1, 2, 3, 4, 6, 12 e 15), li ho messi in fila belli
ordinati, e ho indicato quali sono la loro media, mediana e moda.
Chi fa statistica, in effetti, distingue ben tre tipi di media (in
inglese, "average"); non è un loro vezzo, ma una necessità. Parleranno
pertanto di media, mediana e moda: in inglese, i
nomi sono rispettivamente mean, median e mode. La
media è quella che tutti noi ci si aspetta, vale a dire la media
aritmetica: si fa la somma dei elementi tra cui fare la media, si
divide il risultato per il numero degli elementi stessi, e quello che
esce fuori è la media. La mediana si calcola invece mettendo in
fila tutti gli elementi, e prendendo il valore di quello di mezzo; se il
numero di elementi presenti è pari, e quindi non c'è "quello di mezzo",
si prendono i due "più di mezzo" e si fa la loro media aritmetica. Resta
infine la moda, detta anche norma, che è la meno intuitiva;
eppure il suo significato è logico. Quando si dice che una cosa è "di
moda"? Quando la usano tutti. Allo stesso modo, la moda di un gruppo
di elementi è il valore che capita più spesso. Nel caso ci siano due
o più valori con lo stesso numero di occorrenze, generalmente si dice
che la moda non è definita; d'altra parte, se esiste, è sicuramente
un valore tra quelli osservati, mentre la media non è detto lo sia e la
mediana lo è sicuramente solo nel caso di un numero dispari di elementi in
totale. Tanto per aggiungere un disegnino, nella figura di destra ho preso
alcuni numeri (1, 1, 1, 2, 3, 4, 6, 12 e 15), li ho messi in fila belli
ordinati, e ho indicato quali sono la loro media, mediana e moda. Anche gli ingegneri, poi, non volevano essere da meno e si
sono inventati ancora un altro tipo di media, che chiamano media
quadratica oppure valore efficace. Questo tipo di media è
utile ad esempio nel caso si voglia calcolare la media di tensione della
corrente alternata. La fregatura della corrente alternata è che a volte
la tensione è positiva e a volte negativa: se si fa la media aritmetica
viene fuori zero, e chiunque si sia preso una scossa capisce che c'è
qualcosa che non va. Un approccio naïf potrebbe essere quello di prendere
il valore assoluto di tensione e fare la media di quello; ma gli ingegneri
- nonostante affermino il contrario - non amano le semplificazioni e
hanno così pensato a un approccio più complicato. Per calcolare la media
quadratica si prendono i vari valori, li si eleva al quadrato
(capito il motivo del nome?), si fa la media dei nuovi valori ottenuti
e si estrae la radice quadrata del tutto. In effetti, a dirla così, la
cosa sembra davvero un'inutile complicazione: ma gli ingegneri hanno un
asso nella manica e dicono che questo tipo di media tiene anche in conto
quanto i dati sono dispersi... ma di questo ne parlerò un'altra volta,
anche perché dire il vero non è che la cosa mi convinca troppo.
Anche gli ingegneri, poi, non volevano essere da meno e si
sono inventati ancora un altro tipo di media, che chiamano media
quadratica oppure valore efficace. Questo tipo di media è
utile ad esempio nel caso si voglia calcolare la media di tensione della
corrente alternata. La fregatura della corrente alternata è che a volte
la tensione è positiva e a volte negativa: se si fa la media aritmetica
viene fuori zero, e chiunque si sia preso una scossa capisce che c'è
qualcosa che non va. Un approccio naïf potrebbe essere quello di prendere
il valore assoluto di tensione e fare la media di quello; ma gli ingegneri
- nonostante affermino il contrario - non amano le semplificazioni e
hanno così pensato a un approccio più complicato. Per calcolare la media
quadratica si prendono i vari valori, li si eleva al quadrato
(capito il motivo del nome?), si fa la media dei nuovi valori ottenuti
e si estrae la radice quadrata del tutto. In effetti, a dirla così, la
cosa sembra davvero un'inutile complicazione: ma gli ingegneri hanno un
asso nella manica e dicono che questo tipo di media tiene anche in conto
quanto i dati sono dispersi... ma di questo ne parlerò un'altra volta,
anche perché dire il vero non è che la cosa mi convinca troppo.